Skip to main content

Study Guide

Field 222: Multi-Subject: Teachers of Childhood
(Grade 1 to Grade 6)
Part Two: Mathematics

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

Expand All | Collapse All

Sample Selected-Response Questions

The following reference material will be available to you during the test:

Formulas PDF

Competency 0001 
Number and Operations

1. A bag contains a number of plastic disks that are either red, green, or blue. One-quarter of the disks are red and two-thirds of the disks are green. Which is a possible value for the number of disks in the bag that are either red or green?

  1. 18
  2. 36
  3. 42
  4. 88
Enter to expand or collapse answer. Answer expanded
Correct Response: D. This question requires the examinee to perform operations on fractions. Add the portions that are red and green:  one fourth plus two thirds equals three twelfths plus eight twelfths equals eleven twelfths  so 11/12  eleven twelfths  of all the disks are either red or green. Since there must be a whole number of disks, the total number of disks must be a multiple of 12, and for every 12 disks, 11 of them are either red or green, so the number of red and green disks must be a multiple of 11. The only multiple of 11 given is 88.

Competency 0001 
Number and Operations

2. What is the solution set of the system of linear equations below?

 3 x plus y equals 3 halves 

 x plus y equals 2 

  1.  open paren 1 fourth comma 9 fourths close paren 
  2.  open paren negative 1 fourth comma 9 fourths close paren 
  3.  open paren 5 fourths comma 9 fourths close paren 
  4.  open paren negative 5 fourths comma 9 fourths close paren 
Enter to expand or collapse answer. Answer expanded
Correct Response: B. This question requires the examinee to solve pairs of simultaneous linear equations. The system shown can be solved using the linear combination method by first subtracting the two equations:
 3 x plus y equals 3 halves 
 minus open paren x plus y equals 2 close paren 
 2 x equals negative 1 half 
The result is  2 x equals negative 1 half . Next solve for x by dividing both sides by 2, thus  x equals negative 1 fourth . Replace x with  negative 1 fourth  in the second equation, yielding  negative 1 fourth plus y equals 2 . Solve for y by adding  1 fourth  to both sides, resulting in y equals 2 plus 1 fourth equals 8 fourths plus 1 fourth equals 9 fourths. The solution set of the system of equations is  open paren negative 1 fourth comma 9 fourths close paren .

Competency 0001 
Number and Operations

3. Given that a, b, c, and d are all negative integers, which statement is true?

  1.  the quantity a plus b over the quantity a plus c equals b over c  
  2.  a over b minus c over d equals the quantity a minus c over the quantity b minus d 
  3.  a over c divided by b over d equals the quantity a divided by b over the quantity c divided by d 
  4.  a times b over c equals the quantity a times b over the quantity a times c 
Enter to expand or collapse answer. Answer expanded
Correct Response: C. This question requires the examinee to apply and extend understanding of operations with fractions to add, subtract, multiply, and divide rational numbers. To determine  a over c divided by b over d  , multiply the first fraction by the reciprocal of the second fraction. That is,  a over c divided by b over d equals a over c times d over b which equals a d over b c . To determine  the quantity a divided by b over the quantity c divided by d , rewrite the numerator and denominators as fractions. That is,  the quantity A divided by b over the quantity c divided by d equals open paren a over b close paren over open paren c over d close paren which equals a over b divided by c over d which equals a over b times d over c which equals a d over b c  . Because  a over c divided by b over d equals a d over b c  and  the quantity a divided by b over the quantity c divided by d equals a d over b c ,  a over c divided by b over d equals the quantity a divided by b over the quantity c divided by d   for all nonzero values a, b, c, and d.

Competency 0002 
Ratios and Proportional Relationships and Number Systems

4. Use the diagram below to answer the question that follows.

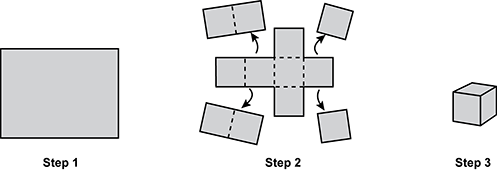
a diagram with three labeled images

step one is one large rectangle that is wider then tall step two shows the pieces that are removed to create a pattern for a box taking the original large rectangle and separating it into twelve equas squares with four columns and three rows you would remove the two top left squares and the two bottom left squares you would also remove the top right square and the bottom right square step three shows the box that was created by folding what was left in step two.

The steps for making a cube-shaped box by cutting and folding a rectangular piece of paper are shown in the diagram. If all the small squares shown in step 2 are congruent and the volume of the box produced in step 3 is 216 cubic units, what is the area of the rectangular sheet of paper in step 1?

  1. 72 square units
  2. 144 square units
  3. 432 square units
  4. 864 square units
Enter to expand or collapse answer. Answer expanded
Correct Response: C. This question requires the examinee to use cube roots to solve problems. Working backward, if the volume of the cube in step 3 is 216 cubic units, then  216 equals e cubed,  where  e equals the length of one edge of the cube,  and  e equals sup 3 the square root of 216  or 6. Each of the squares shown in step 2 has an edge of 6, so each square has an area of  6 times 6,  or 36. There are 12 squares that make up the rectangle, so the area of the rectangle is  12 times 36 equals 432  square units.

Competency 0002 
Ratios and Proportional Relationships and Number Systems

5. Use the graphs below to answer the question that follows.

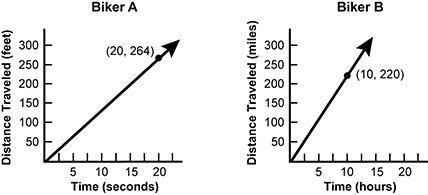
two graphs of distance traveled over time of biker A and B

Two graphs are shown. One graph is titled Biker A and the other graph is titled Biker B. On the graph titled Biker A, the x axis is labeled time open paren seconds close paren and has evenly distributed tick marks labeled 5, 10, 15, 20. The y axis is labeled distance travelled open paren feet close paren and has evenly distributed tick marks labeled 50, 100, 150, 200, 250, 300. The graph titled Biker A has a straight line that starts at 0 comma 0 and passes through a point labeled 20 comma 264. On the graph titled Biker B, the x axis is labeled time open paren hours close paren and has evenly distributed tick marks labeled 5, 10, 15, 20. The y axis is labeled distance travelled open paren miles close paren and has evenly distributed tick marks labeled 50, 100, 150, 200, 250, 300. The graph titled Biker B has a straight line that starts at 0 comma 0 and passes through a point labeled 10 comma 220.

Based on the information shown in the graphs, which value is closest to the difference in miles per hour between the speeds of the two bikers?

  1. 8.8  miles per hour  
  2. 10.2  miles per hour  
  3. 13.0  miles per hour  
  4. 19.0  miles per hour  
Enter to expand or collapse answer. Answer expanded
Correct Response: C. This question requires the examinee to solve unit rate problems, including those involving constant speed. The graph for Biker A shows that the biker traveled 264 feet in 20 seconds. Determine the unit rate for Biker A by dividing 264 feet by 20 seconds to obtain 264 divided by 20 equals 13.2 feet per second. Use dimensional analysis to convert 13.2 feet per second to miles per hour; that is,  13.2 feet over 1 second times 1 mile over 5280 feet times 3600 seconds over 1 hour equals the quantity 13.2 times 3600 over 5280 miles per hour equals 9 miles per hour. The graph for Biker B shows that the biker traveled 220 miles in 10 hours, so determine the unit rate for Biker B; that is, 220 divided by 10 equals 22 miles per hour. The difference between the two speeds is 22 minus 9 equals 13 miles per hour.

Competency 0003 
Algebra, Measurement, Geometry, and Data

6. Use the diagram below to answer the question that follows.

ruler consisting of twelve inches and thirty centimeters

Which expression can be used to estimate the number of feet in 2 kilometers?

  1. start fraction numerator one thousand times one hundred times two denominator two times five times twelve end fraction feet
  2. start fraction numerator two times one thousand times two denominator five times twelve times one hundred end fraction feet
  3. start fraction numerator two times one thousand times one hundred times two denominator five times twelve end fraction feet
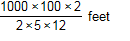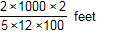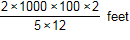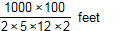  4. start fraction numerator one thousand times one hundred denominator two times five times twelve times two end fraction feet
Enter to expand or collapse answer. Answer expanded
Correct Response: C. This question requires the examinee to solve problems involving conversions of measurement units. Using an estimate of  5 centimeters equals 2 inches   1000 meters equals 1 kilometer ,  100 centimeters = 1 meter  and  1 foot equals 12 inches , set up a multiplication of ratios so that the units "cancel": start fraction numerator two kilometers denominator one end fraction times start fraction numerator one thousand meters denominator one kilometer end fraction times start fraction numerator one hundred centimeters denominator one meter end fraction times start fraction numerator two inches denominator five centimeters end fraction times start fraction numerator one foot denominator twelve inches end fraction

Competency 0003 
Algebra, Measurement, Geometry, and Data

7. Use the system of equations below to answer the question that follows.

 negative 2 x plus 3 y equals 8 
 7 x minus 6 y equals negative 2 

Which equation is a step in solving the system for x by using elimination?

  1.  3 x equals 6 
  2.  3 x equals 14 
  3.  11 x equals negative 18 
  4.  11 x equals negative 10 
Enter to expand or collapse answer. Answer expanded
Correct Response: B. This question requires the examinee to solve systems of equations in two variables. Solving this system of equations for x using the elimination, or linear combination, method will eliminate the y variable. First, multiply both sides of the equation  negative 2 x plus 3 y equals 8  by 2, resulting in   negative 4 x plus 6 y equals 16   Next, add this resulting equation to   7 x minus 6 y equals negative 2   to obtain   open paren negative 4 x plus 6 y close paren plus open paren 7 x minus 6 y close paren equals 16 plus negative 2  , which simplifies to 3 x equals 14.

Competency 0003 
Algebra, Measurement, Geometry, and Data

8. Use the table below to answer the question that follows.

x  f of x 
negative 2negative 1
negative 10
02
14
28
35
4negative 2

A partial table of the function  f of x  is shown. What is the value of   the quantity negative f of 1 + 2 f of 2 all over f inverse of negative 2   ?

  1. 3
  2. 4
  3. 6
  4. 12
Enter to expand or collapse answer. Answer expanded
Correct Response: A. This question requires the examinee to apply the concept of a function and use function notation appropriately. The table shows the values of the ordered pairs   open paren x comma f of x close paren   To find the value of   f of x   locate x in the first column and read across to the second column for the value of f of x. The value of   f of 1 equals 4. The value of negative f of 1 equals negative 4. The value of f of 2 = 8, and the value of 2 f of 2 equals 2 times 8 equals 16. The value of the numerator of the fraction is negative 4 plus 16 equals 12.

The symbol f inverse of x represents the inverse of f of x. To find the inverse of a table of values, switch the values in the first column with the values in the second column. The table for f inverse of x will have the following table.

x   f inverse of x  
  negative  1  negative  2
0  negative  1
20
41
82
53
  negative  24

The new table shows the values of the ordered pairs   open paren x comma f inverse of x close paren  . To find the value of   f inverse of negative 2  , find   negative  2 in the first column and read across to the second column. The value of   f inverse of negative 2 equals 4  , so the denominator of the fraction equals 4.

The value of   the quantity negative f of 1 + 2 f of 2 all over f inverse of negative 2 equals 12 fourths equals 3  .

Competency 0004 
Instruction in Mathematics

9. A third-grade teacher is preparing to teach the following standard from the New York State Learning Standards for Mathematics. footnote 1 

Number & Operations—Fractions (NY-3.NF)

Develop understanding of fractions as numbers.

3. Explain equivalence of fractions, and compare fractions by reasoning about their size.

Which strategy is likely to be most effective as part of an introductory lesson designed to meet this standard?

  1. teaching that  one third  is equivalent to  two sixths  by showing how they represent the same point on a number line
  2. teaching that  one third  is equivalent to  two sixths  because  one third times two halves equals two sixths  according to the rules of fractions
  3. teaching that  one third  is equivalent to  two sixths  because 6 is the least common denominator of 2 and 3
  4. teaching that  one third  is equivalent to  two sixths  by showing cross multiplication of  1 times 6 equals 2 times 3 
Enter to expand or collapse answer. Answer expanded
Correct Response: A. This question requires the examinee to apply strategies for extending understanding of fractions, equivalence, and ordering. The key words here are  start italics compare fractions by reasoning about their size end italics . The position of a number on a number line is a representation of its size, so showing that two fractions represent the same point on a number line shows that they are the same size and therefore are equivalent fractions.

Competency 0004 
Instruction in Mathematics

10. Which activity would best help a first-grade student develop a background for understanding congruence?

  1. composing and decomposing plane figures into composite figures
  2. recognizing figures from different perspectives and orientations
  3. determining the measurable attributes of objects
  4. modeling two-dimensional shapes by drawing
Enter to expand or collapse answer. Answer expanded
Correct Response: B. This question requires the examinee to demonstrate knowledge of strategies for teaching how to compare, create, and compose shapes and how to analyze attributes of shapes, including symmetry and properties of their lines and angles. Recognizing that shapes in different orientations can be the same size and shape lays the groundwork for understanding congruence.

Acknowledgments

1From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Internet. Available from http://www.nysed.gov/curriculum-instruction/new-york-state-next-generation-mathematics-learning-standards; accessed 2/20/2019.