Study Guide

Field 163: Physics

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

Expand All | Collapse All

Sample Selected-Response Questions

The following reference materials will be available to you during the test:

Physics Reference Materials

Competency 0001 
Forces and Motion

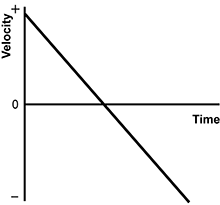
1. The velocity-time graph below represents the motion of a particle moving in one dimension.

A velocity versus time graph is shown. The x-axis (horizontal) is labeled Time and the y- axis (vertical) is labeled Velocity. The x-axis intersects the middle of the y axis at zero. Reading from left to right on the graph, a diagonal line starts at a high positive velocity value. The line has a constant slope, crosses the middle of the x axis, and ends at high value of negative velocity.

Which statement best describes the motion of the particle at the time the graphed line crosses the time axis?

1. The particle is located at the origin.
2. The acceleration of the particle is changing.
3. The particle is changing direction.
4. The acceleration of the particle is zero.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: C. This question requires examinees to analyze and describe a graph of motion in one or two dimensions using multiple representations. The velocity versus time graph provides information about the direction and magnitude of the particle's motion. At t = 0, the velocity of the particle is positive and the particle is traveling in the positive direction but is slowing down. When the line crosses the t-axis, the velocity of the particle is 0. After crossing the time axis, the graph indicates that the particle is traveling in the negative direction. The point where the graphed line crosses the time axis indicates when the particle's velocity changed direction from positive to negative.

---

Competency 0001 
Forces and Motion

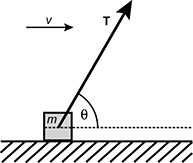
2. As shown in the diagram below, a 20. kg mass, m, is pulled by a rope across a rough horizontal surface at constant velocity, v. The tension in the rope is 50. N and the angle, θ theta , is 60.° degrees  above the horizontal.

A force diagram is shown. A rightward, horizontal arrow labeled italic v is in the top left corner. A small box labeled italic m is on a flat, horizontal surface. The tail of a vector labeled boldface T is in the middle of the box. The vector points to the right and forms an angle, theta, with a dotted, horizontal line that is parallel to the level surface on which the box is located.

What is the coefficient of sliding friction between the mass and the surface?

1. 0.13
2. 0.16
3. 0.22
4. 0.26

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: B. This item requires examinees to analyze and evaluate situations involving frictional forces using multiple representations. Since the mass in the problem is moving with constant velocity, the net horizontal force on the mass is 0 N. The net vertical force on the mass is also 0 N. The tension force has both vertical and horizontal components given by:

T_y = T sin 60.° = (50. N)(0.866) = 43 N and T_x = T cos 60.° = (50. N)(0.50) = 25 N.

The magnitude of the frictional force (F_f) must equal the horizontal component of the tension (T_x), so F_f = T_x. The frictional force on the box is also directly proportional to the normal force (F_N) and is F_f = µF_N, where µ is the coefficient of friction. Therefore, µ = ^F_f/_FN. Since the tension in the rope has a vertical component, F_y, the normal force of the mass on the surface is given by:

F_N = mg − F_y, and F_N = (20. kg)(9.8 m/s²) − 43 N = 153 N.

The coefficient of sliding friction is given by:

µ = ^F_f/_FN = ^{25 N}/_{153 N} = 0.16.

T subscript Y equals T sine sixty degrees equals fifty point N multiplied by zero point eight six six equals forty three N, and T subscript X equals T cosine sixty degrees equals fifty point N multiplied by zero point five zero equals twenty five N. The magnitude of the frictional force parenthesis F subscript f close parenthesis must equal the horizontal component of the tension parenthesis T subscript X close parenthesis, so F subscript f equals T subscript X. The frictional force on the box is also directly proportional to the normal force parenthesis F subscript N close parenthesis and is F subscript f equals mu F subscript N, where mu is the coefficient of friction. Therefore mu equals F subscript F divided by F subscript N. Since the tension in the rope has a vertical component, F subscript Y, the normal force of the mass on the surface is given by F subscript N equals M G minus F subscript Y, and F subscript N equals twenty point K G multiplied by nine point eight M per S squared minus forty three N equals one hundred fifty three N. The coefficient of sliding friction is given by mu equals F subscript f over F subscript N equals twenty five N over one hundred fifty three N equals zero point one six.

---

Competency 0002 
Conservation of Energy and Energy Transfer

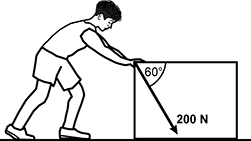
3. A person pushes a box a distance of 4.0 m across a rough horizontal surface. The person applies a force of 200 N in the direction shown. The box starts from rest and has a final kinetic energy of 100 J.

A person and a box on a flat horizontal surface are shown. The person is on the left and is pushing on the top left corner of the box where the tail of a vector labeled boldface two hundred N is drawn. The vector points downward with a negative slope. The tip of the vector is near the bottom middle of the box. The vector forms a sixty degree angle with the horizontal top of the box.

Line	Work Done by Person (J)	Work Done by Friction (J)
1	800	− negative 700
2	800	− negative 100
3	400	− negative 300
4	400	− negative 100

Which line in the table correctly identifies the total amount of work done by the person on the box and the total amount of work done by friction?

1. Line 1
2. Line 2
3. Line 3
4. Line 4

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: C. This question requires examinees to analyze and evaluate situations involving work, energy, and power, including energy flow and conservation, using multiple representations. Given an applied force of 200 N at an angle of 60° with the horizontal, its horizontal component is:

F_x = (F_applied)(cos 60°) = (200 N)(0.50) = 100 N.

Because the object moves in the horizontal direction only, the work done by the person is given by:

W_applied = F_x Δd = (100 N)(4.0 m) = 400 J.
(Alternatively, W_applied = F_applied Δd cos 60° = (200 N)(4.0 m)(0.50) = 400 J.)

Applying the law of conservation of energy, the magnitude of the work done by friction equals applied work minus final energy: W_friction = W_applied – E_final. Therefore, the magnitude of the work done by friction is:

W_friction = 400 J − 100 J = 300 J.

F subscript X equals F subscript applied multiplied by cosine sixty degrees equals two hundred N multiplied by zero point five zero equals one hundred N. Because the object moves in the horizontal direction only, the work done by the person is given by W subscript applied equals F subscript X times delta D equals one hundred N multiplied by four point zero M equals four hundred J. Open parenthesis. Alternatively, W subscript applied equals F subscript applied times delta D cosine sixty degrees equals two hundred N multiplied by four point zero M multiplied by zero point five zero equals four hundred J. Close parenthesis. Applying the law of conservation of energy, the magnitude of the work done by friction equals applied work minus final energy: W subscript friction equals W subscript applied minus E subscript final. Therefore, the magnitude of the work done by friction is: W subscript friction equals four hundred J minus one hundred J equals three hundred J.

The direction of the work done by friction is opposite to the direction of the work done by the person, so friction does negative work. These results agree with the information in Line 3 of the table.

---

Competency 0002 
Conservation of Energy and Energy Transfer

4. Students release a solid cylinder and a thin hoop from rest at the top of an inclined plane. The two objects have the same mass and radius and roll without slipping down the plane. The students measure the time required for the cylinder and the hoop to roll down the plane for several trials and record the average values as shown in the table below.

	Cylinder	Hoop
Average Time Required	6.7 s	7.2 s

Which statement about the mechanical energy of the two objects at the bottom of the plane best follows from these results?

1. The total kinetic energy of the cylinder is less than the total kinetic energy of the hoop.
2. The linear kinetic energy of the hoop is greater than the linear kinetic energy of the cylinder.
3. Not all of the potential energy of the hoop was converted to kinetic energy.
4. A higher proportion of potential energy is converted to rotational kinetic energy for the hoop than for the cylinder.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: D. This question requires examinees to analyze and draw inferences from experimental data, scientific and technical texts, and graphics; to interpret graphs and data; to apply mathematical and computational thinking in analyzing data; and to evaluate the hypotheses, data, analyses, and conclusions in a scientific or technical text related to the conservation of energy and energy transfer. The gravitational potential energy of both the thin hoop and the solid cylinder are the same at the top of the inclined plane. At the bottom of the plane, both objects have the same total mechanical energy, assuming no frictional losses. The total kinetic energy at the bottom is equal to the sum of the translational kinetic energy of the center of mass and the rotational kinetic energy of the object, given by:
KE_Total = ¹/₂mv² + ¹/₂Iω².  K E subscript Total equals one half M V squared plus one half I omega squared 
The translational velocity of the cylinder was greater than for the hoop, since it traveled the same distance in a shorter time. Therefore, the cylinder's translational kinetic energy was also greater. From this, it follows that a greater proportion of the hoop's mechanical energy was converted into rotational kinetic energy.

---

Competency 0003 
Electricity and Magnetism

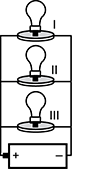
5. The diagram below represents a circuit containing three identical lightbulbs and an ideal battery.

An image is shown of a circuit. The bottom of the image shows a battery with a positive sign on the left and a negative sign on the right. Lines indicating wires connect each side of the battery to each of three light bulbs above it. There are no loads along the circuit until the circuit branches into three paths. Each path has one light bulb. After the light bulbs, the paths reconnect and the circuit is completed. The light bulb directly above the battery is labeled roman numeral 3, the light bulb above it is labeled roman numeral 2, and the top light bulb is labeled roman numeral 1.

Which statement best explains what will happen if bulb III 3  burns out?

1. Bulb I 1  and bulb II 2  will emit more light than before because the total resistance of the circuit will decrease.
2. Bulb I 1  and bulb II 2  will emit more light than before because the current through the circuit will remain the same.
3. Bulb I 1  and bulb II 2  will emit the same amount of light as before because the voltage across the bulbs will remain the same.
4. Bulb I 1  and bulb II 2  will emit the same amount of light as before because the total power supplied by the battery will remain the same.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: C. This question requires examinees to demonstrate conceptual knowledge of a complete circuit, current, and voltage. The circuit consists of three identical lamps connected in parallel with an ideal battery. In this arrangement, the voltage across each lamp is the same as the battery voltage, and each lamp is independent from the others. The currents through each lamp must be the same, since each lamp has the same applied voltage, and the lamps are identical with the same resistance. If Bulb III 3  burns out, its branch of the circuit becomes an open circuit with no current. This change has no effect on the operation of the remaining two lamps, since they still receive the original applied voltage, and their resistances have not changed.

---

Competency 0003 
Electricity and Magnetism

6. A proton has a mass of 1 u and a charge of +1e. A beam of protons, with each proton having velocity v, enters a magnetic field and undergoes uniform circular motion of radius r. An alpha particle has a mass of 4 u and a charge of +2e. A beam of alpha particles enters the same magnetic field with the same initial velocity as the protons. What is the radius of the circular path for this beam of alpha particles?

1. ¹/₂1 half r
2. 2r
3. 4r
4. 8r

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: B.

This question requires examinees to analyze the motion of charged particles in electric and magnetic fields to predict their direction and pathways. The magnitude of the centripetal force acting on a particle traveling with uniform circular motion is given by F_c = ^mv2/_r, where F_c is the force, m is the mass of the particle, v is the particle's velocity, and r is the radius of the circular path. The magnitude of the magnetic force on a charge q is F = qvB sinθ, where B is the magnitude of the magnetic field and θ is the angle between v and B. Since the particle is undergoing uniform circular motion, it follows that the magnetic field is perpendicular to the velocity of the charge, so the equation simplifies to F = qvB. Combining the two force equations and solving for the radius of the path followed by the charge gives:

r = ^mv/_qB.

In this problem, v and B are the same for both particles. The radius of the path of the proton is:

r_proton = ^{(1 u)v}/_{(1 e)B}.

The radius of the path of the alpha particle is:

r_alpha = ^{(4 u)v}/_{(2 e)B} = 2r_proton.

This question requires examinees to analyze the motion of charged particles in electric and magnetic fields to predict their direction and pathways. The magnitude of the centripetal force acting on a particle traveling with uniform circular motion is given by F subscript C equals M V squared over R, where F subscript C is the force, M is the mass of the particle, V is the particle's velocity, and R is the radius of the circular path. The magnitude of the magnetic force on a charge Q is F equals Q V B sine theta, where B is the magnitude of the magnetic field and theta is the angle between V and B. Since the particle is undergoing uniform circular motion, it follows that the magnetic field is perpendicular to the velocity of the charge, so the equation simplifies to F equals Q V B. Combining the two force equations and solving for the radius of the path followed by the charge gives R equals M V divided by Q B. In this problem, V and B are the same for both particles. The radius of the path of the proton is R subscript proton equals open parenthesis one U close parenthesis V divided by open parenthesis one E closed parenthesis B. The radius of the path of the alpha particle is: R subscript alpha equals open parenthesis 4 U closed parenthesis V divided by open parenthesis two E closed parenthesis B equals two R subscript proton.

---

Competency 0004 
Mechanical Wave Properties

7. Students are exploring waves using a simulation of a wave propagating on a long string driven at one end by an oscillator. The simulation allows the students to change three parameters and observe the results. Which setting will produce the wave with the greatest speed?

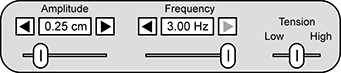1. A set of three sliders labeled amplitude, frequency, and tension is shown. The amplitude slider is set at zero point two five C M. The frequency slider is set at three point zero zero H Z. The tension slider is set in between low and high.


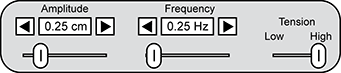2. A set of three sliders labeled amplitude, frequency, and tension is shown. The amplitude slider is set at zero point two five C M. The frequency slider is set at zero point two five H Z. The tension slider is set on high.


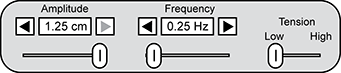3. A set of three sliders labeled amplitude, frequency, and tension is shown. The amplitude slider is set at one point two five C M. The frequency slider is set at zero point two five H Z. The tension slider is set on low.


4. A set of three sliders labeled amplitude, frequency, and tension is shown. The amplitude slider is set at one point two five C M. The frequency slider is set at three point zero zero H Z. The tension slider is set in between low and high.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: B. This question requires examinees to demonstrate knowledge of mechanical wave properties, including propagation and speed, and what constitutes a wave. The speed of a wave on a string is given by:
v = ,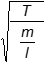
where v is the wave speed, T is the magnitude of the tension in the string, and ^m/_lm over l is the mass per unit length of the string. The wave speed is independent of amplitude and frequency. The highest tension setting will produce the greatest wave speed.

---

Competency 0004 
Mechanical Wave Properties

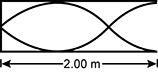
8. The diagram below represents a standing wave in a pipe of length 2.00 m filled with air and open at one end.

If the speed of sound in air is 340. m/s, what is the frequency of the sound wave produced?

1. 113 Hz
2. 127 Hz
3. 170. Hz
4. 255 Hz

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: B. This question requires examinees to analyze and evaluate patterns and characteristics of standing waves using multiple representations. The resonant standing wave pattern illustrates ³/₄3 fourths of a wavelength in a 2.00 m long pipe with one end closed. Therefore, the wavelength for this tone is:

^{2.00 m}/_{0.750 cycle}1 third = 2.67 m.

The frequency is given by: f = ^v/_λv over lambda, where f is the frequency in Hz, v is the wave speed in m/s, and λ lambda  is the wavelength in m. Solving this equation gives:

f = ^{340. m/s}/_{2.67 m}340. meters per second over 2.67 meters = 127 Hz.

---

Competency 0005 
Optics and Electromagnetic Waves

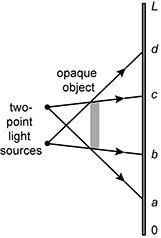
9. The diagram below shows a ray diagram for the shadow formed on a screen of length L by two light sources and an opaque object.

A ray diagram of two light sources shining on an opaque object and onto a screen is shown. The two point light sources are on the left and one is above the other. A narrow, vertical screen is on the right and the screen is labeled L, D, C, B, A, 0 from top to bottom. An opaque, vertical object is in the middle. The height of the opaque object is much less than the height of the screen. Each light source has two rays extending from it. From the top light source, one ray extends slightly diagonally upward, touching the top of the opaque object and continuing to point C on the screen. From the top light source, the other light ray extends diagonally downward, touching the bottom of the opaque object and continuing to point A on the screen. From the bottom light source, one ray extends diagonally upward, touching the top of the opaque object and continuing to point D on the screen. From the bottom light source, the other light ray extends slightly diagonally downward, touching the bottom of the opaque object and continuing to point B on the screen.

Several points are indicated along the screen. Which graph best represents the relative light intensity along the screen?

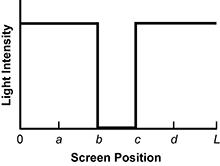1. A light intensity versus screen position graph is shown. The X axis is labeled Screen Position and the Y axis is labeled Light Intensity. Reading from left to right on the graph, the Screen Position axis is labeled 0, A, B, C, D, L at equally spaced intervals. At Screen Position 0, a horizontal line starts at a high light intensity. The line continues to Screen Position B, where it becomes vertical and drops to very low light intensity. The line is horizontal at very low light intensity between screen positions B and C. At C, the line becomes vertical, rises back to high light intensity, and becomes horizontal. The line continues at high light intensity, ending at Screen Position L.


2. A light intensity versus screen position graph is shown. The X axis is labeled Screen Position and the Y axis is labeled Light Intensity. Reading from left to right on the graph, the Screen Position axis is labeled 0, A, B, C, D, L at equally spaced intervals. At Screen Position 0, a horizontal line starts at a high light intensity. The line continues to Screen Position A, where it becomes vertical and drops to very low light intensity. The line is horizontal at very low light intensity between screen positions A and D. At D, the line becomes vertical, rises back to high light intensity, and becomes horizontal. The line ends at Screen Position L.


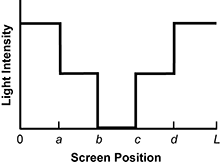3. A light intensity versus screen position graph is shown. The X axis is labeled Screen Position and the Y axis is labeled Light Intensity. Reading from left to right on the graph, the Screen Position axis is labeled 0, A, B, C, D, L at equally spaced intervals. At Screen Position 0, a horizontal line starts at a high light intensity. The line continues to Screen Position A, where it becomes vertical and drops to medium light intensity. The line is horizontal at medium light intensity between screen positions A and B. At B, the line becomes vertical and drops to very low light intensity. The line is horizontal at very low light intensity between screen positions B and C. At C, the line becomes vertical, rises back to medium intensity, and becomes horizontal. The line is horizontal at medium light intensity between C and D. At D, the line becomes vertical, rises back to high light intensity, and becomes horizontal. The line ends at Screen Position L.


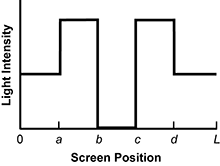4. A light intensity versus screen position graph is shown. The X axis is labeled Screen Position and the Y axis is labeled Light Intensity. Reading from left to right on the graph, the Screen Position axis is labeled 0, A, B, C, D, L at equally spaced intervals. At Screen Position 0, a horizontal line starts at medium light intensity. The line continues to Screen Position A, where it becomes vertical and rises to high light intensity. The line is horizontal at high light intensity between screen positions A and B. At B, the line becomes vertical and drops to very low light intensity. The line is horizontal at very low light intensity between screen positions B and C. At C, the line becomes vertical, rises back to high light intensity, and becomes horizontal. The line is horizontal at high light intensity between C and D. At D, the line becomes vertical, drops back to medium light intensity, and becomes horizontal. The line ends at Screen Position L.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: C. This question requires examinees to analyze the behavior of light in the presence of opaque objects using ray diagrams. The light rays shown for the two sources define the edge limits of illumination and shadow regions produced by the opaque object. In the regions L to d and 0 to a, light rays from both sources will illuminate the screen and the observed intensities will add. In the regions d to c and a to b, only rays of light from one source will illuminate the screen. The observed light intensity in these regions will be less. In the region from b to c, there will be no light from the two sources illuminating the screen, and the intensity of the light there will be a minimum or zero.

---

Competency 0005 
Optics and Electromagnetic Waves

10. In his Book of Optics, Ibn al-Haytham (c. circa  965– to c. circa  1040) presents a theory of light. He states that light must be a type of movement, because its velocity is reduced in a denser medium and that the refracted ray always takes the quickest and easiest path. This indicates an understanding of the concepts associated with which formula?

1. ^sinθ₂/_sinθ1 = ^v₂/_v1 = ^n₁/_n2  sine theta subscript 2 over sine theta subscript 1 equals V subscript 2 over V subscript 1 equals N subscript 1 over N subscript 2 
2. θ_B = arctan ^n₂/_n1  theta subscript B equals arctangent open parenthesis N subscript 2 over N subscript 1 close parenthesis  
3. c² = a² + b² − 2ab cos γ C squared equals A squared plus B squared minus 2 A B cosine gamma  
4. cos²γ + sin²γ cosine squared gamma plus sine squared gamma   = 1

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: A. This question requires examinees to analyze wave refraction using multiple representations. Ibn al-Haytham states that the velocity of a light ray entering a denser medium is reduced. The velocities of light in different media are inversely proportional to the index of refraction, n, of the media through which they travel. This gives: v₁ = ^c/_n1 and v₂ = ^c/_n2, V subscript 1 equals C over N subscript 1 and V subscript 2 equals C over N subscript 2 where v₁ and v₂ V subscript 1 and V subscript 2  are the velocities of light, c is the speed of light in a vacuum, and n is the index of refraction. The angles of incidence and refraction associated with rays of light passing from one medium into another are measured with respect to the normal line that is perpendicular to the surface of the material. The law of refraction (Snell's law) states that the ratio of the sines of the angles of incidence and refraction is equal to the ratio of the velocities of light in the two media, and is given by:

^sinθ₂/_sinθ1 = ^v₂/_v1 = ^n₁/_n2 sine theta subscript 2 over sine theta subscript 1 equals V subscript 2 over V subscript 1 equals N subscript 1 over N subscript 2.

---

Competency 0005 
Optics and Electromagnetic Waves

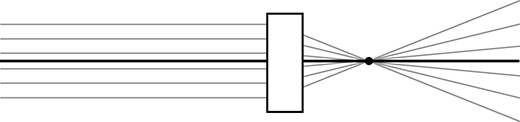
11. The diagram below shows parallel rays of light incident on a lens.

An image of light entering and exiting a boxed region is shown. A blank boxed region is located in the middle of the image. A dark horizontal line runs through the middle of the image, except in the boxed region, indicating the optical axis of the system. To the left of the boxed region, three parallel, horizontal light lines run above and parallel to the dark horizontal line. To the left of the boxed region, three parallel, horizontal light lines run below and parallel to the dark horizontal line. To the right of the boxed region, three nonparallel diagonal light lines run downward from the upper right side of the boxed region to converge at a common point denoted by a dot on the dark horizontal line. To the right of the boxed region, three nonparallel diagonal light lines run upward from the lower right side of the boxed region to converge at the common point denoted by the dot on the dark horizontal line. To the right of the dot, each of the six diagonal light lines continue with the same slope it had before entering the dot. These six light lines fan out with different constant slopes on the far right side of the image.

Four lenses with equal heights are shown.

The first, leftmost lens is rectangular. Its height is about four times its width. It is equal in height to all the other lenses. The second lens from the left is equal in height to all the other lenses. Both its left and right sides curve inward toward its center. Its width is greatest at its top and its bottom and its width is least in its middle. Its height is about four times its maximum width and about five times its minimum width. The third lens from the left has the same height as the other lenses and is much thinner. Its left side curves slightly inward toward its center. Its right side curves outward, away from its center, with a greater degree of curvature than its left side. Its width is maximum at its center and its top and its bottom are points. Its height is about eight times its maximum width. 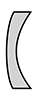The fourth, rightmost lens has the same height as the other lenses. Its left side curves outward, away from its center. Its right side curves inward, toward its center. The degree of curvature of its right side is greater than the degree of curvature of its left side. Its width is greatest at its top and its bottom and its width is least in its middle. Its height is about four times its maximum width and about five times its minimum width.

[On an actual exam, the examinee would see the following directions and would have the ability to click on one of the above lenses, drag it to the designated area in the diagram above, and drop it into place. The examinee would be able to change lenses until they are satisfied with their choice.]

Drag and drop the lens that will create the ray pattern shown into the designated area in the diagram.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: Plano-convex lens.

An image of light entering and exiting a boxed region is shown. The boxed region is located in the middle of the image. A dark horizontal line runs through the middle of the image, except in the boxed region. To the left of the boxed region, three parallel, horizontal light lines run above and parallel to the dark horizontal line. To the left of the boxed region, three parallel, horizontal light lines run below and parallel to the dark horizontal line. Inside the boxed region is the third lens from the left. Its left side curves slightly inward toward its center. Its right side curves outward, away from its center, with a greater degree of curvature than its left side. Its width is maximum at its center and its top and its bottom are points. Its height is about eight times its maximum width. To the right of the boxed region, three nonparallel diagonal light lines run downward from the upper right side of the boxed region to converge at a common point denoted by a dot on the dark horizontal line. To the right of the boxed region, three nonparallel diagonal light lines run upward from the lower right side of the boxed region to converge at the common point denoted by the dot on the dark horizontal line. To the right of the dot, each of the six diagonal light lines continue with the same slope it had before entering the dot. These six light lines fan out with different constant slopes on the far right side of the image.

This question requires examinees to analyze the behavior of light in mirrors and lenses using multiple representations. A qualitative application of the law of refraction (Snell's law) to simple lenses illustrates the effect of refraction on the path of light rays as they pass through transparent material. When passing through single or double convex lenses, light rays converge at a distance from the center of the lens defined as the focal point. When passing through transparent materials having concave surfaces, light rays diverge as they exit the material. The only lens shown that will produce converging rays of light is the plano-convex lens.

---

Competency 0006 
Modern Physics

12. Experiments demonstrating the photoelectric effect seemed to violate classical physics. Which outcome was resolved by assuming that light is quantized?

1. The light incident on a metal surface caused electrons to be ejected from the surface.
2. The kinetic energy of emitted electrons was independent of the light intensity.
3. The charge of the emitted electrons always had the same fundamental value.
4. The stopping potential could be used to determine the maximum kinetic energy of the electrons.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: B. This question requires examinees to demonstrate knowledge of the observations and reasoning necessitating the particulate nature of light. Classical electromagnetism predicted that the kinetic energy of the electrons ejected from a metal surface due to light incident on the surface should be proportional to the intensity of the light. As light intensity increased, the kinetic energy of the emitted electrons should increase. However, experiments indicated that the kinetic energy of the electrons was independent of the intensity of the incident light. As the intensity of the light increased, the number of electrons emitted increased, but not the kinetic energy of the electrons. Einstein resolved this issue by postulating that a beam of light of frequency f consists of a stream of photons, each of which carries a quantized amount of energy given by: E = hf. It follows from this postulate that the kinetic energy of the emitted electrons is independent of the intensity of the light.

---

Competency 0006 
Modern Physics

13. In an electron gun, electrons undergo positive acceleration across a potential difference V. Which graph best represents how the de Broglie wavelength of the electrons depends on V?

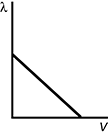1. A lambda versus V graph is shown. The X axis is labeled V and the Y axis is labeled lambda. Reading from left to right on the graph, a line starts about halfway up the Y axis. The line is diagonal with a constant slope of about negative one. The line ends on the X axis, about two thirds of the distance from the origin to the end of the X axis.


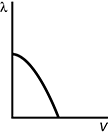2. A lambda versus V graph is shown. The X axis is labeled V and the Y axis is labeled lambda. Reading from left to right on the graph, a curve starts about halfway up the Y axis. The curve starts with zero slope and immediately its slope becomes negative. The curve forms the shape of the right half of the top of an inverted parabola before ending about halfway along the X axis.


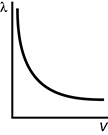3. A lambda versus V graph is shown. The X axis is labeled V and the Y axis is labeled lambda. Reading from left to right on the graph, a curve starts near the top of the Y axis, but does not touch the axis. The curve starts with negative slope near infinity and immediately the magnitude of its slope decreases. The curve's slope is about negative one at about one fourth of the distance from the origin to the end of the X axis. The magnitude of the curve's slope continues to decrease, reaching close to zero at the end of the X axis. The curve does not touch the X axis


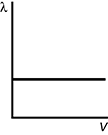4. A lambda versus V graph is shown. The X axis is labeled V and the Y axis is labeled lambda. Reading from left to right on the graph, a horizontal line starts about one third of the way up the Y axis. The line is perfectly horizontal with zero slope, and continues until the right edge of the graph.

Answer Enter to expand or collapse answer. Answer expanded

Correct Response: C. This question requires examinees to demonstrate knowledge of basic principles of quantum mechanics. The de Broglie wavelength of an electron is λ lambda = ^h/_ph over p, where λ lambda  is the wavelength in meters, h is Planck's constant, and p is the momentum of the particle. The electron's velocity, v, and thus its momentum, mv, increases with the potential difference, V, that accelerates the electron. Therefore, as the potential difference increases, the momentum increases and the de Broglie wavelength, λ lambda , decreases.

---

Copyright © 2019 by the New York State Education Department