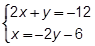Study Guide
Field 232: Multi-Subject: Teachers of Middle Childhood
(Grade 5–Grade 9)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Constructed-Response Item 1
Competency 0004
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the task that follows. end bold
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Exhibit 1: Background Information
Sixth-grade students have been developing their understanding of the concept of a ratio. The class has been using ratio language to describe simple situations, such as the ratio of the number of tires on a bicycle to the number of bicycles. The class is currently working on the following standard from the New York State Learning Standards for Mathematics.1 Acknowledgments 1
start bold Ratios & Proportional Relationships (6.RP) end bold
start bold A. Understand ratio concepts and use ratio reasoning to solve problems. end bold
1. Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
The teacher has planned a lesson experience in which students will make measurements using various units and use ratio language to describe the relationships between the measurement units.
Exhibit 2: Description of Class Activity
The teacher divides students into pairs and gives each pair of students a container filled with paper clips, erasers, and craft sticks. The students first measure the length of a tissue box using the craft sticks. The students then measure the length of the same tissue box using the erasers and then the paper clips. Each student records the measurements in his or her own notebook.
The teacher then collects the craft sticks and the paper clips, leaving the students with only the erasers. The students next measure the length of a table using the erasers. The teacher asks the students to use ratio language to describe the relationship between the measurement units and express the measurement of the length of the table in units of craft sticks and paper clips.
Exhibit 3: Excerpt of Interview with Student
As students work, the teacher moves among them and asks questions that require students to justify their reasoning using viable arguments. The teacher stops to observe one pair's work in progress. One student's measurements are shown below.
objects are laid end to end horizontally showing that they all are equal in length there are six paper clips four erasers two craft sticks and one tissue box
The teacher looks at the student's measurements and asks to see what she has recorded in her notebook. The student's notebook contains the following statements.
The box is 2 craft sticks long.
The box is 4 erasers long.
The box is 6 paper clips long.
The table is 8 erasers long.There are 4 erasers for every 2 craft sticks. Halve the number of erasers to get the number of craft sticks. The table is 8 erasers long so it's 4 craft sticks long.
There are 4 erasers for every 6 paper clips. Increase the number by 2 to go from erasers to paper clips. The table is 8 erasers long so it is 10 paper clips long.
After reading the student's notes, the teacher asks the student several questions about the activity. A short excerpt of the discussion between the teacher and the student is shown below.
Teacher: How did you find the relationship between erasers and craft sticks? Student: We saw that there was double the number of erasers as craft sticks while measuring the tissue box. So to go from erasers to craft sticks we had to find the half. If you have 8 erasers, that's the same length as 4 craft sticks. Teacher: OK, so if you measured a length that was 12 erasers long, how many craft sticks long would it be? Student: Well, the craft sticks are longer, so if it's 12 erasers long, take half of 12 to get 6. It would be 6 craft sticks long. Teacher: That's good. Can you use ratio language to describe the ratio of the number of erasers to craft sticks? The ratio of erasers to craft sticks is what to what? Student: Let's see, the ratio of erasers to craft sticks is 4:2 because for every 4 erasers there are 2 craft sticks. The conversation continues on this topic. Later the teacher asks the following question.
Teacher: How did you find the relationship between erasers and paper clips? Student: When we were measuring the tissue box, we saw that it takes 4 erasers and 6 paper clips. In this case, they're not just double so you need to add 2 more paper clips than erasers. So that means that we need to add 2 to go from erasers to paper clips. Teacher: Suppose you measured an object that was 8 erasers long. How many paper clips long would it be? Student: You would need 10 since you need 2 more paper clips than erasers. That means that the ratio of paper clips to erasers is 6:4 because there are 2 more paper clips than erasers.
Sample Strong Response to Constructed-Response Item 1
The student shows strength in her understanding of the concept of using a ratio to describe a relationship between two quantities. When looking at the eraser measurement and the craft stick measurement of the tissue box, the student writes "there are 4 erasers for every 2 craft sticks," and correctly sees that the number of craft sticks is half the number of erasers. In order to find the number of craft sticks equal to 8 erasers, the student says "we had to find the half." This idea was extended to another example converting a length of 12 erasers to 6 craft sticks. The student also could write and understand ratio language to describe the ratio of number of erasers to number of craft sticks, and appreciated the importance of order when describing the ratio numerically. The ratio "4 to 2" was used "because for every 4 erasers there are 2 craft sticks."
The student demonstrates an area of need when she reasons additively rather than multiplicatively to create equivalent ratios when the numbers did not work out as half or double. Stating "4 erasers for every 6 paper clips, increase the number by 2 to go from erasers to paper clips" when finding the number of paper clips needed for 8 erasers shows additive reasoning. The student noted that in this case, the numbers were not double, necessitating the decision to use a different technique to solve the problem. She erroneously reasoned that adding 2 to 8 results in 10 paper clips for the length of the table.
Instructional intervention should start with the student drawing a diagram showing 4 erasers for every 2 craft sticks, as understanding the ratio between the two items was a strength for her. Then, using other manipulatives (pencils, scissors, etc.) to create several other ratios equivalent to 4 erasers for every 2 craft sticks, iterate the diagram to illustrate these new ratios. To be sure that the student is not simply using doubling for every ratio problem, examples where the ratio of one unit to another is 3 to 1 or 5 to 1, rather than 2 to 1 should be included. Next the student should do the same activity for the original ratio of erasers to paper clips. Both the manipulatives and the diagrams will help the student to visualize the multiplicative nature of the process. As the new ratios are created, the teacher should ask for explanation of how they were found and justification that the ratios are equivalent.
A next step would be to have the student use a data table to record results, using one column to keep track of number of erasers, and the second column for number of paper clips. Using a pattern, the student should extend the table. Plotting the data on a graph would help the student look for any errors in the table. Following up with other problems where the ratio numbers are not half or double, such as 2 to 7 or 8 to 3 would help solidify the student's proportional thinking.
As a final step, the student should have to explain why the ratio of 4 erasers to 6 paper clips is not equivalent to the ratio of 8 erasers to 10 paper clips using diagrams, tables and graphs to justify her reasoning. The multiplicative nature of equivalent ratios requires the student to have a certain level of mathematical maturity. Having the student manipulate physical objects, plot data, and explain her thinking will help her build a viable argument related to ratios and proportions.
Sample Constructed-Response Item 2
Competency 0004
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the task that follows. end bold
Using the data provided, prepare a response of approximately 400–600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Exhibit 1: Background Information
A teacher is working with a student in an eighth-grade mathematics class. The class is currently working on the following standard from the New York State Learning Standards for Mathematics.2Acknowledgments 2
start bold Expressions, Equations, and Inequalities (NY-8.EE) end bold
start bold Analyze and solve linear equations and pairs of simultaneous linear equations. end bold
8b. Solve systems of two linear equations in two variables with integer coefficients: graphically, numerically using a table, and algebraically. Solve simple cases by inspection.
In particular, the teacher gave an assignment following a class period during which students practiced solving systems of two linear equations by using substitution and elimination strategies.
Exhibit 2: Student Work Sample
The class's assignment was to complete ten problems related to solving systems of two linear equations. Shown below are three sample problems from the assignment, along with the student's response to each problem. Both the problems and the responses are representative of the student's work.
start bold Worksheet Directions: Determine which start uppercase METHOD end uppercase (substitution or elimination) will best solve the system. start uppercase EXPLAIN end uppercase why you chose that method. Then start uppercase SOLVE end uppercase the system. end bold
Problem 1:
- start bold M:Method: end bold substitution
- start bold E:Explain: end bold because y equals m x plus b is easy to plug in
- start bold S:Solve: end bold –2x + 2x + 3 = 6negative 2 x plus 2 x plus 3 equals 6
3 = 6 x false!3 equals 6, wrong, false!
no solutionProblem 2:
- start bold M:Method: end bold elimination
- start bold E:Explain: end bold because both are in standard form
- start bold S: Solve: end bold
2 open paren 5 x plus y equals 2 close paren 10 x plus 2 y equals 4 10 x plus 2 y equals 4 negative 10 x plus negative 2 y equals negative 4
0 equals 0, checked, true!
Problem 3:
- start bold M:Method: end bold substitution
- start bold E:Explain: end bold because it's the same as the first one
- start bold S:Solve: end bold 2 open paren negative 2 y minus 6 close paren + y = negative 12
negative 4 y minus 12 plus y equals negative 12
negative 3 y minus 12 equals negative 12
negative 3 y equals 0, wrong, false!
no solution
Exhibit 3: Excerpt of Interview with Student
Shown below is an excerpt of an interview between the teacher and the student during which the teacher questions the student about the method of solution used to solve the problems shown in the student work sample.
Teacher: How did you set up Problem 1? Student: I saw that the first equation was in y equals m x + b form, so that means I need to use substitution. I plugged in 2 x plus 3 into y in the second equation because that's what y equals in the first equation. Teacher: Why did you say there was no solution? Student: The 2x's cancel out, so that leaves 3 equals 6, which is false. If it's false, it means it can't ever be true, so there are no solutions. Teacher: Okay. Tell me about Problem 2. What did you do here? Student: This is different because all the x's and y's line up, so that means they're in standard form and you should use elimination. I wanted the y's to cancel because those have smaller numbers in front, so they're easier, so I multiplied the equation by 2. Teacher: Where did these negative numbers come from, right here in this second equation? Student: The y's need to cancel, and the only way for them to do that is to be the same but opposites. That means I needed to change the sign of everything in the first or second equation—it doesn't really matter which one. And actually, that made it so the y's and the x's canceled. Teacher: Good. Let's look at Problem 3. Student: It's basically the same thing as the first problem. I plugged it in. Tried to solve for y and got negative 3 y equals 0, which is false, so no solutions.
Sample Strong Response to Constructed-Response Item 2
One significant strength that the student exhibits is in understanding of how to solve linear equations using the elimination method. He is able to explain why this is the correct method to use ("because both are in standard form"), and knew he needed to get one set of coefficients to be additive inverses. He then successfully solved the system, showing that this system worked for this type of set of equations. His explanation to the teacher in the interview is a bit weak, as it is vague and it could be considered unclear that he "needed to change the sign of everything in the first or second equation," but it is evident he understands how to solve linear equations using elimination. In addition, the student also knows when to use the substitution method. While he does not correctly answer question number 3, he has accurately used this method in both problems 1 and 3.
An area of need arises when the student fails to finish the third problem, concluding that it is false and there is no solution. He stops at negative 3 y equals 0 not completely solving for y. The student can take this one additional step, and divide each side by negative 3 which will give him an answer of y equals 0 but he seems to have forgotten that any multiplication problem which produces a product of 0 must contain a 0. This would make y equals 0 It seems the student has a problem with understanding multiples of 0.
To help this student, I would review with him that all multiplication problems with a product of 0 need to have 0 as one of the multiples. We would practice some of these together to reinforce that he understands this. In addition, I would ask him what the next step would be in solving the equation he has left to solve, -3y=0. It’s possible that since part of the equation contains a negative number, this may be throwing him off, so I will review with him what the next step would be if the problem read: 3 y equals 0 He should know that 3 y translates to 3 times y ( 3 times y ), and to solve for y, you need to divide by 3 on each side. I would have him do this and note that in this case, y equals 0 We would then review the rule again, remembering that the same is true whether the multiple is a positive or negative number. Once we have reviewed this, the student should be able to explain that regardless of whether the multiple is positive or negative, if the product is 0, then y would be equal to 0. He should then be able to note that the equation does, in fact, have a solution, in this case, y equals 0 and x equals negative 6 I would have him practice this with similar equations until he is comfortable in his explanation.
Performance Characteristics for a Constructed-Response Item
The following characteristics guide the scoring of the response to a constructed-response item.
| Completeness | The degree to which the response addresses all parts of the assignment |
|---|---|
| Accuracy | The degree to which the response demonstrates the relevant knowledge and skills accurately and effectively |
| Depth of Support | The degree to which the response provides appropriate examples and details that demonstrate sound reasoning |
Score Scale for a Constructed-Response Item
A score will be assigned to the response to a constructed-response item according to the following score scale.
| Score Point | Score Point Description |
|---|---|
| 4 |
The "4" response reflects a thorough command of the relevant knowledge and skills:
|
| 3 |
The "3" response reflects a general command of the relevant knowledge and skills:
|
| 2 |
The "2" response reflects a partial command of the relevant knowledge and skills:
|
| 1 |
The "1" response reflects little or no command of the relevant knowledge and skills:
|
| U | The response is unscorable because it is unrelated to the assigned topic or off task, unreadable, written in a language other than English or contains an insufficient amount of original work to score. |
| B | No response. |
Acknowledgments
1 From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Internet. Available from http://www.nysed.gov/curriculum-instruction/new-york-state-next-generation-mathematics-learning-standards; accessed 1/8/2019.
2 Ibid.
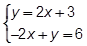
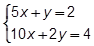
 true!
true!